“La Ecuación de Lorentz… pero como nunca antes te la habían contado”

¿Y si pudiéramos entender la ecuación de Lorentz sin recurrir a la rutina de las fórmulas clásicas? En este primer artículo del blog, proponemos un enfoque diferente, alejada del tratamiento clásico basado en postulados de Einstein y transformaciones directas. A través de un razonamiento distinto, mostramos cómo llegar al mismo resultado desde una perspectiva más conceptual, revelando nuevas conexiones entre la física y la geometría del espacio-tiempo.

ENSAYO SOBRE LAS ECUACIONES DE LORENTZ

La posición- tiempo (x',t')   en función de (x,t), las podemos expresar:

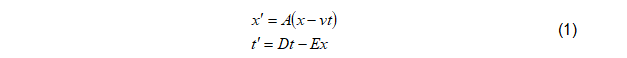
La primera de las ecuaciones hemos considerado que será de la misma forma que en Mecánica Clásica multiplicada por una constante, mientras que la segunda ecuación consideramos que el tiempo en movimiento dependerá de la posición y del tiempo en reposo.

            La segunda consideración que vamos a tener en cuenta es que la velocidad de la luz es la misma en el sistema de referencia en reposo y movimiento, es decir:

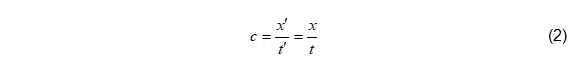
Al expresar las dos ecuaciones (2) en función del tiempo, teniendo en cuenta (2) tenemos:

Dividiendo las dos ecuaciones (3) resulta:

Al ser la velocidad de la luz constante, para que se cumpla (4) se ha de cumplir:

Llevando los valores (5) a (1) quedan:

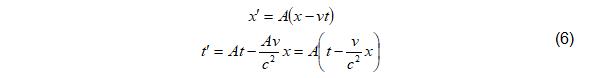
Expresiones similares a las (6) serán las expresadas (x,t) en función de (x',t'):

Sustituyendo en la primera de las ecuaciones (7) los valores de x' y t' obtenidos en (6):

El valor (8) sustituido en (6) nos dan las ecuaciones de Lorentz:

Las expresiones anteriores las he obtenido mediante 3 constantes. Pero el nuevo planteamiento es considerar que la relación entre los sistemas de referencia O y O', las coordenadas de cada evento  vienen dadas por (x,y,z,t) y (x',y',z',t'), donde y=y', z=z', moviéndose el eje x en la misma dirección que el eje x' y con una velocidad constante v.  La transformación lineal más sencilla entre (x , t) y (x', t') más sencilla será:        

      Si en la primera de las ecuaciones (10) consideramos fijo el origen de O' y que el móvil es O, la distancia que recorre en un tiempo t, el origen O es x=vt, siendo x'=0: